NEW GENERATION - ==> Summenformel von Gauß

Diese Summenformel wie auch die Summenformel für die ersten $n$ Quadratzahlen war bereits in der vorgriechischen Mathematik bekannt.

Carl Friedrich Gauß entdeckte diese Formel als neunjähriger Schüler wieder. Die Geschichte ist durch Wolfgang Sartorius von Waltershausen überliefert:

„Der junge Gauss war kaum in die Rechenclasse eingetreten, als Büttner die Summation einer arithmetischen Reihe aufgab. Die Aufgabe war indess kaum ausgesprochen als Gauss die Tafel mit den im niedern Braunschweiger Dialekt gesprochenen Worten auf den Tisch wirft: »Ligget se’.« (Da liegt sie.)“

– Wolfgang Sartorius von Waltershausen^[1]

Die genaue Aufgabenstellung ist nicht überliefert. Oft wird berichtet, dass Büttner die Schüler die Zahlen von 1 bis 100 (nach anderen Quellen von 1 bis 60) addieren ließ und Gauß feststellte, dass die erste und die letzte Zahl (1+100), die zweite und die vorletzte Zahl (2+99) usw. zusammen immer 101 ergeben. Der Wert der gesuchten Summe ergibt sich so zu 101 mal 50.

Entsprechend den damaligen Verhältnissen unterrichtete Büttner etwa 100 Schüler in einer Klasse. Damals waren auch Züchtigungen mit der sogenannten Karwatsche (Karbatsche, Lederpeitsche) üblich. Sartorius berichtet: „Am Ende der Stunde wurden darauf die Rechentafeln umgekehrt; die von Gauss mit einer einzigen Zahl lag oben und als Büttner das Exempel prüfte, wurde das seinige zum Staunen aller Anwesenden als richtig befunden, während viele der übrigen falsch waren und alsbald mit der Karwatsche rectificirt wurden.“^[2] Büttner erkannte bald, dass Gauß in seiner Klasse nichts mehr lernen konnte.

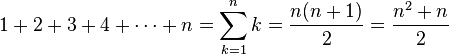
1 + 2 + 3 + 4 + \dotsb + n = \sum_{k=1}^n k = \frac{n(n+1)}{2} = \frac{n^2+n}{2}

Diese Reihe ist ein Spezialfall der arithmetischen Reihe, und ihre Summen

1, 3, 6, 10, \dotsc

werden Dreieckszahlen genannt.

Auch der folgenden Aufgabe kann die Formmel angewendet werden:

In dem Billard-Turnier hat es 12 Spieler: jeder spielt gegen jeden.
wieviel Spiele müssen gemacht werden?

Herangehensweise: 1. Überlegung: Wenn jeder gegen jeden spielt, somit muss jeder
                                     Spieler 11 Spiele machen.
                                     - das ist richtig -, weil man ja nicht gegen sich selbst spielen kann.

man könnte denken: "Ha, da haben wir es ja schon: is ja ganz einfach 11*12=132, leider
falsch gedacht, denn:

                                 2. Überlegung:
                                      Wir verkürzen auf 4 Spieler: ABCD, jeder gegen jeden:

                                 3. Überlegung:
                                      Spieler A fängt an:
                                      A gegen B, A gegen C, A gegen D   ===> A hat alle drei Spiele
                                                                                                          und hat gegen jeden ge-
                                                                                                          spielt.
                                      Spieler B macht weiter: B kann nicht gegen sich selbst spielen und
                                       und hat schon gegen A gespielt, folglich muss er noch zwei Spiele
                                      machen. B muss noch gegen C und D spielen.

                                      Spieler C ist dran: Er kann nicht gegen sich selbst und hat bereit
                                      A und B gespielt folglich hat er nur noch 1 Spiel gegen D zu tun.

                                      Jetzt kommt D dran und siehe : D kann nicht gegen sich selbst
                                      spielen und hat bereit gegen A, B und C gespielt, wie oben zu
                                      lesen ist. Folglich hat er kein Spiel mehr zu machen. Jeder hat
gegen jeden gespielt und jeder hat 3 Spiele gemacht.

                                  A , B , C, D

                               1. A --> B , A --> C, A --> D

                               2.                B --> C , B --> D

                               3.                                C --> D

                               4.        Kein Spiel zu machen

            Wie oben kann man die Dreieckentwicklung schön sehen.

             Überlegung 4: Wie setze ich jetzt die gegeben Werte in die Formel ein?
                                     Es sind die Anzahl der Spieler gegeben.
                                     Als Ergebnis möchte ich die Anzahl der Spiele haben.

                                    Das heißt ich addiere die Anzahl der Spiele mit der Formel
                                    von Gauß, je nach Nachfolger nehmen die Spiele um 1 ab, weil
                                    man schon ein Spiel bei dem Vorgänger mit gemacht hat , oder
                                    zwei bei dem Vor-, Vorgänger.

                                    Wir sagen also Anzahlt der Spieler ist n, wie gegeben 12.

            Formel:           Sigma i=0 bis n-1, n-1 weil man nicht gegen sich selbst spielen
                                    kann. Warum Null ( Null ist das neutrale Element der Addition),
                                    weil der letzte Spieler ( also n) kein Spiel mehr zu tun hat, weil er
                                    bei den anderen Spielen dabei ist)

                                     In die Formel einsetzen: (n-1)(n-1+1)/2


Rechnung: n=12 wie oben:      (12-1)(12-1+1)/2 = 66 Spiele